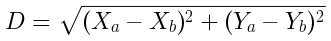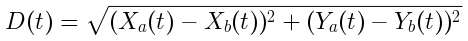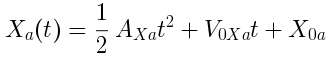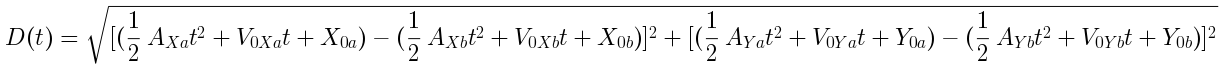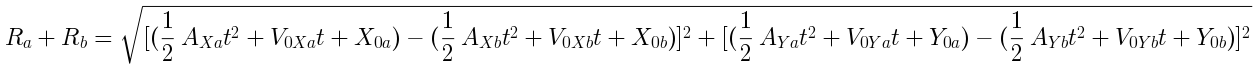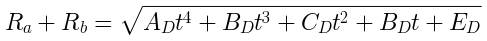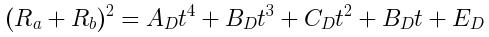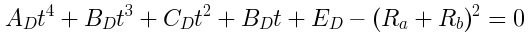Predicting Circle Intersections

Fall Free!

I've been working on a game called Fall Free. I'm starting this blog to reflect on interesting challenges, approaches, and solutions that have come up during development.

For this first post I’m starting with predicting intersections between moving objects. This was my original inspiration for getting into game development. I am planning to write about more topics in future posts.

The idea of predicting intersections ahead of time — as opposed to detecting and reacting to intersections that have already happened — somehow got stuck in my head. It seemed like an interesting math puzzle for its own sake and maybe a basis for interesting game mechanics.

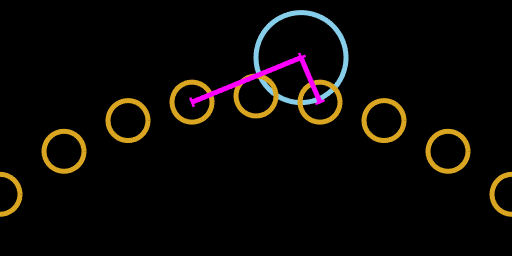
So here's how I approached the problem and implemented a solution for Fall Free. For the game engine this became the basis of the data and events model. For the player, the same prediction events are visualized as space pod “sensors”.

Fall Free pod sensors

Moving Circles

I based the predictions on moving circles. Circular symmetry is really handy, making a 2D system feel almost 1D. This simplified some of the algebra below. It also helped when building up from circles to more complex shapes like polygons, which is a topic I'll save for a future post.

I modeled motion over time as 2D, quadratic. Linear motion would have been a much simpler choice. But quadratic felt like a natural way to express the the motion of a space pod under constant acceleration from its thrusters. Even better, quadratic functions are "curvy" enough to approximate sinusoidal or rotational motion and this was a key to supporting predictions between rotating, extended bodies. I'll write more about that in another post, too.

So this model has circles moving in a plane, with quadratic motion over time in each direction X and Y.

orange circle moving quadratically in 2D

Distance Formula

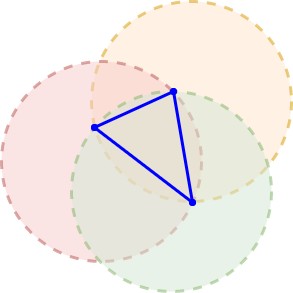
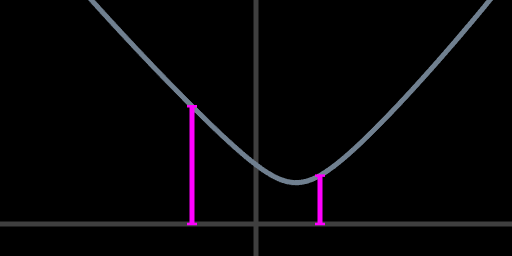
As a start towards predicting intersections, we can simply measure the distance between circle centers. The familar Euclidean/Pythagorean distance formula encodes what we need for D (magenta), the distance between two circle centers a and b.

magenta distance between orange and light blue circle centers

This works when the circle centers X_a Y_a and X_b Y_b are plain old numbers. We can take it a step further by allowing X_a(t) Y_a(t) and X_b(t) Y_b(t) to vary as functions of time. This gives D(t) that we can plot over time, and manipulate below.

distance D(t) between two circles centers over time

To complete the description of D(t), we can define each of the four functions on the right hand side: X_a(t) Y_a(t) and X_b(t) Y_b(t).

I chose these to be quadratic with parameters describing projectile motion along each dimension: an acceleration A an initial velocity V₀ and an initial position X₀ or Y₀. All four functions have the same form, for example this is X_a(t).

In all we have four functions with this same form, and among them are 12 quadratic coefficients to keep track of. I'm using capital letters A V₀ X₀ and Y₀ to indicate terms of each quadratic. I'm using subscripts X or Y to indicate the spatial dimension, and additional subscripts a or b to indicate which object.

It's a lot to scan visually. But despite the numerous subscripts, the intuitive complexity is perhaps not so high. There's a lot of repeated structure. We might think of each object a or b keeping track of 6 projectile motion parameters for itself. When needed, each object can plug in 6 parameters at a time.

Here's D(t) explicitly, showing all 12 parameters.

Up to here we've described the distance between circle centers. For intersection prediction we want to know when the circles themselves will be tangent, or just about to overlap. For this we can bring in the radii of the circles R_a and R_b. When tangent, the center distance D(t) will be equal to the sum of the radii. This a place where circular symmetry helps a lot -- all we have to do is add the radii together and set that sum equal to the distance formula.

By now the forumla is getting unwieldy. Maybe it doesn't even fit in your browser window. But it's still good because this equality encodes everything we need in order to predict intersections. It encodes the 12 projectile motion parameters for two moving objects, the radial sizes of those objects, and a geometric constraint that defines what a touch point or intersection is.

From here we can go on algebra autopilot. Expanding the polynomial squares and grouping like terms, we get a quartic polynomial in t (ie t⁴) on the right hand side. The new quartic coefficients A_D B_D C_D D_D and E_D are directly computed from the original 12 projectile motion parameters. I won't reproduce all the algebra here, but it was a mechanical process with no new insight required to go from the equality above to its equivalent here.

This form is easier to work with and display.

If we square both sides we can change the ugly square root into a square that's easier to work with -- both symbolically and numerically in terms of CPU instructions. This changes the units from touch-distance to touch-distance-squared, and that's OK. We will be interested in finding times when the touch distance goes to zero, and these times will be the same in either units.

This equality will hold true exactly when the two circles are tangent, and those times will be the interesction times that we're trying to predict.

So when will these times be? They will be at the roots of this final quartic polynomial. Note that the only unknown here is t itself, all the other coefficients can be calculated directly from the projecile motion parameters and sizes of the circles a and b.

Quartic Roots

There are several methods out there for numerically finding polynomial roots. I've had fun and success with a method by Peter Strobach. This is another topic I want to write about in a future post. For this post I'll focus on how I'm interpreting the roots after finding them.

In general a quartic can have up to four real roots. For this application the quartics will have all real coefficients, so the roots will come in pairs: zero, two, or four real roots and respectively four, two, or zero complex roots.

The real roots are the keys for this application, we can interpret them as circle tangent times or intersection touch times. As an aside, I don't know if there's a useful interpretation for the complex roots in this application. For now I'm discarding them.

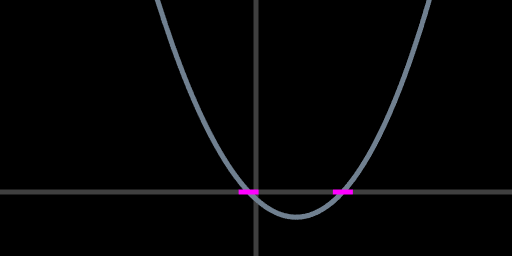
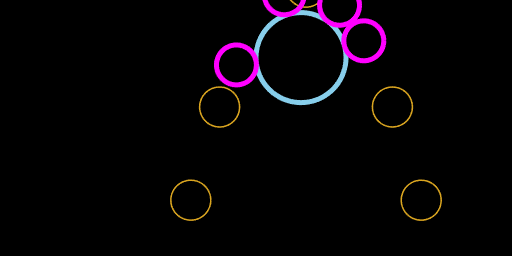
So, once the quartic is solved there are three output cases. The case of two real roots will be familiar from the examples above, where the orange circle approaches the light blue circle, intersects it for an interval, them moves away forever. The two roots of the touch-distance-squared quartic (magenta) correspond to the touch points at the beginning and ending of the intersection inteval.

touch-distance-squared with two real roots (magenta)

orange circle intersecting light blue circle with two magenta touch points

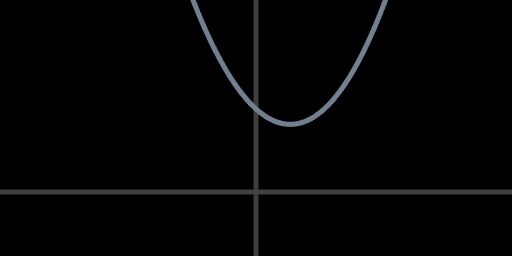
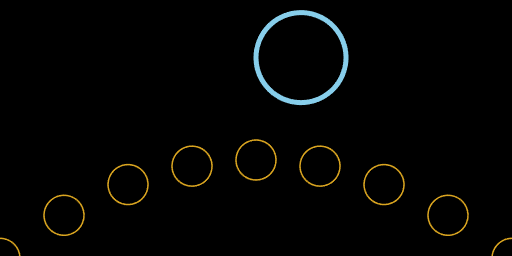
It's also possible for the circles to pass by each other without intersecting. In this case the touch-distance-squared quartic never reaches the horizontal axis, which corresponds to D(t) never getting smaller than the radial distance R_a + R_b.

This is the case of zero real roots and zero touch points.

touch-distance-squared with no real roots

orange and light blue circles that never intersect

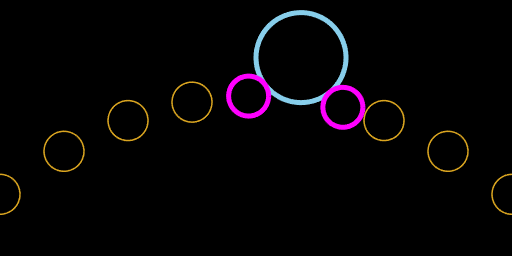
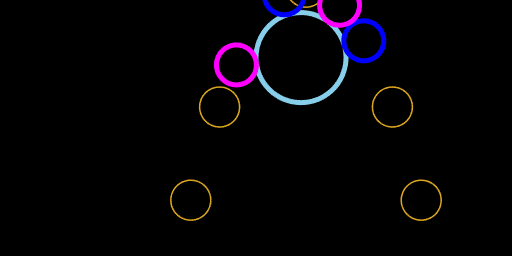
Finally, it's possible for the two circles to intersect twice. In the example below, the first intersection happens as the orange circle moves up and past the light blue circle. Later a second intersection happens as the orange circle falls back down.

This is the case of four real roots, with two roots each for two intersection intervals.

touch-distance-squared with four real roots (magenta)

orange circle intersecting light blue circle twice, with four magenta touch points

Derivative as Metadata

The Fall Free game engine ends up solving a lot of quartics like the ones above and they can be a lot to keep track of. It's not always trivial to choose which touch point is most relevant for a given game mechanic, such as object collisions. It has been useful to annotate each touch point with related metadata like whether it was part of a two-root solution or a four-root solution, or what was the normal direction from one cirlce to the other, at the time of intersection.

One other, very useful annotation is whether the touch point was inward-moving ie the start of an intersection interval, or outward-moving ie the end of an interval. For the example of a collision mechanic, inward-moving touches probably should count as collisions, but outward-moving touches maybe not.

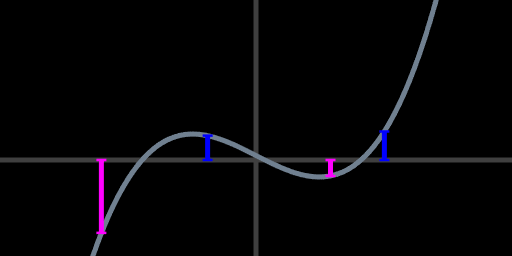
We can check for inward vs outward explicitly, by consulting the derivative of the touch-distance-squared quartic. Since the quartics in this application are generally upwards "U" or "W" shapes, the derivatives are cubic and generally wavy-lines or "Z" shapes moving from the lower left to the top right. Continuing with the four-root example just above, we get a Z-shaped derivative.

derivative of touch-distance-squared evaluated at touch times (magenta and blue)

Reading left to right, the Z-curve starts out negative. This corresponds to the circles initially moving inwards towards each other from far apart. When the curve crosses the horizontal axis to go positive, the circles start moving away from each other. The curve goes negative again temporarily as the circles come together a second time. Finally, the curve goes positive as the circles move outwards and away from each other forever.

To turn this reading into a touch point annotation, we can evaluate the derivative at each of the quartic root touch times. Negative values (magenta) indicate inward-moving, while positive values (blue) indicate outward-moving. We can apply these annotations visually by re-coloring the four circle touch points according to their direction. This might give some intuition that touch points occur in pairs, on either side of an intersection interval.

orange circle intersecting light blue circle twice, with two pairs of magenta and blue touch points

Not that bad!

More to Share

This first post is about my original motivation for making a space pod game with intersection predictions and predictive space pod "sensors".

I wish the game was done and ready to share! Until then, I hope to write more posts about cool topics that come up during the process. Thanks for reading!